哇哦空間設(shè)計(jì) | MIGOCOO服裝店
門外的繁華不是我的繁華,對(duì)于人潮擁擠的地方,如果你不喜歡,繞道便是,沒有那么多是非曲直。如果你簡(jiǎn)單,活的美妙之處在于懂得松弛有度。——木心
▼空間概覽,overall view of the space ?戚朔遷
在人與物皆處在快節(jié)奏、形式化的年代,如何在焦慮的狀態(tài)中尋找內(nèi)心的寧?kù)o?
平靜,不是避開車馬喧囂,而是心中修籬種菊。這一特質(zhì)亦是獨(dú)立設(shè)計(jì)師品牌MIGOCOO的追求,將服飾回歸使用者本身,時(shí)刻關(guān)注質(zhì)感和細(xì)節(jié)。因此,其展廳的思考從空間的“純粹性”契入,強(qiáng)調(diào)體量與幾何,運(yùn)用最基礎(chǔ)元素——體塊、板片與桿件完成空間構(gòu)成。
In a world stuck in fast-forward and conformity,how can we find inner peace in a state of increasing anxiety?
Real peace, not avoid going around, but repairing the fence in the hearts of Chrysanthemum.For MIGOCOO, it is an consistent religionwhich focus on texture and detail and users feeling.We therefore had to think the purity of display space which stress dimension sense and Geometrical relation,Utilize basic elements such as cuboid,flat and rod to defined by specific spatial relationship.
▼以灰色涂料為基底,枯樹干與木球和穿孔不銹鋼搭配調(diào)和整體空間氛圍,構(gòu)成獨(dú)特的空間語言The dead wood、the wood sphere and stainless steel are matched to harmonize the overall space atmosphere ?戚朔遷
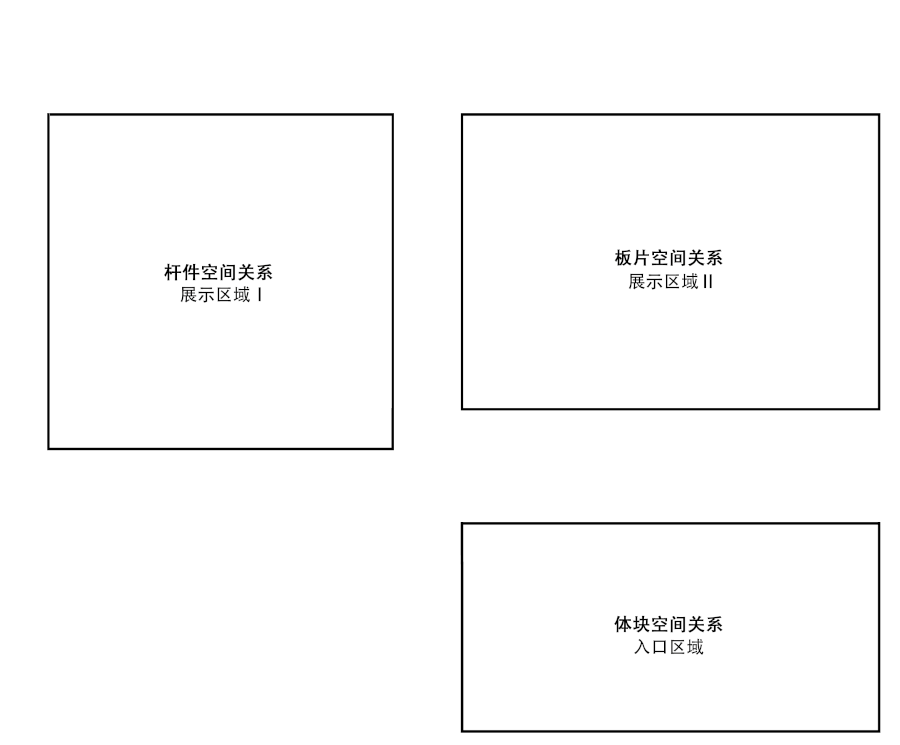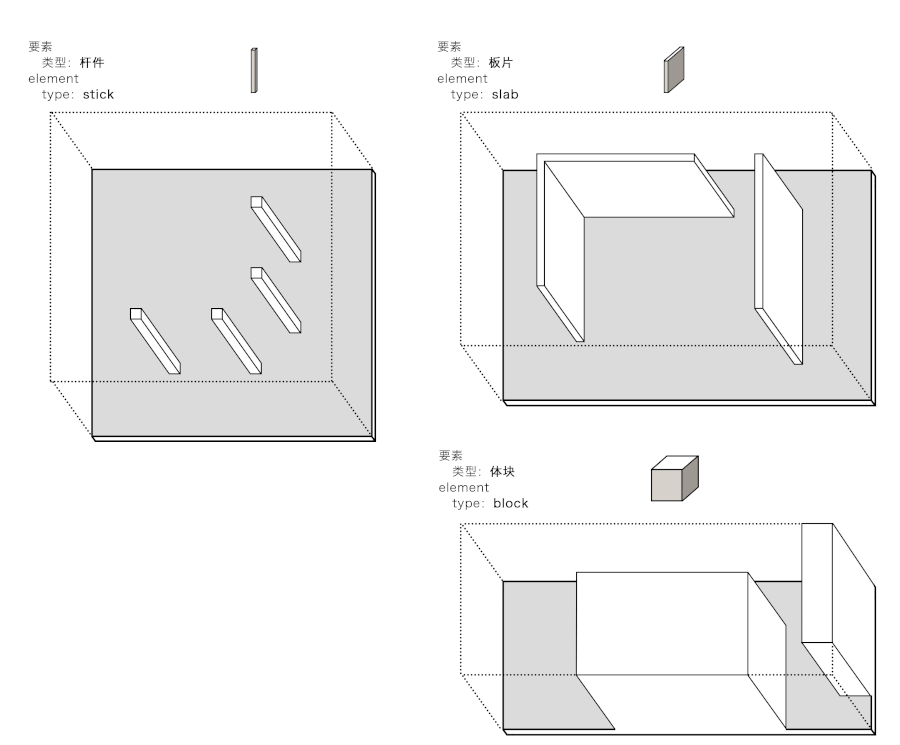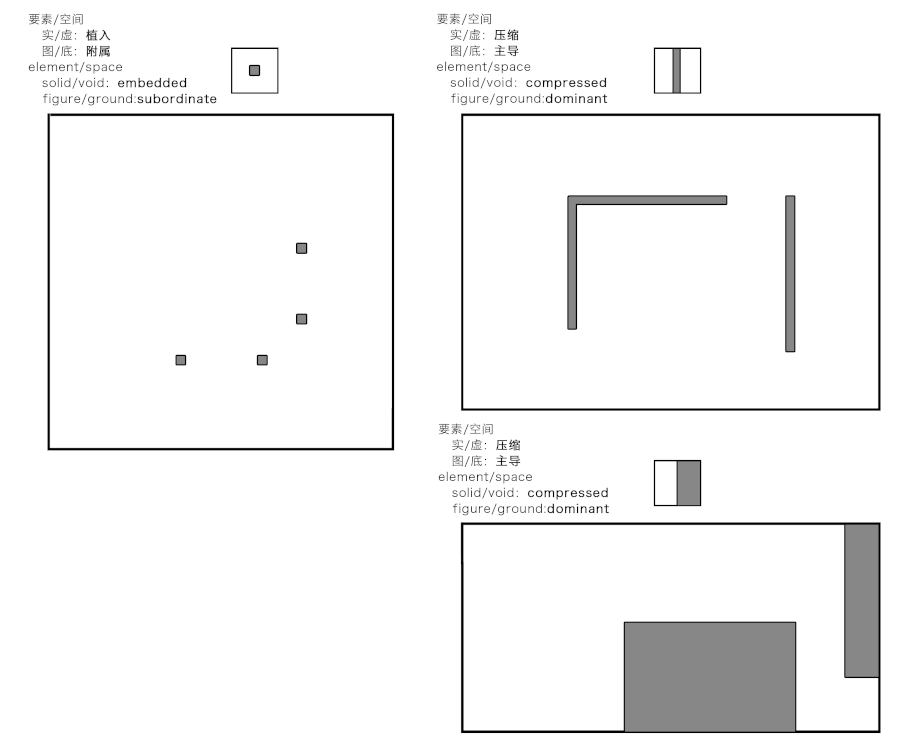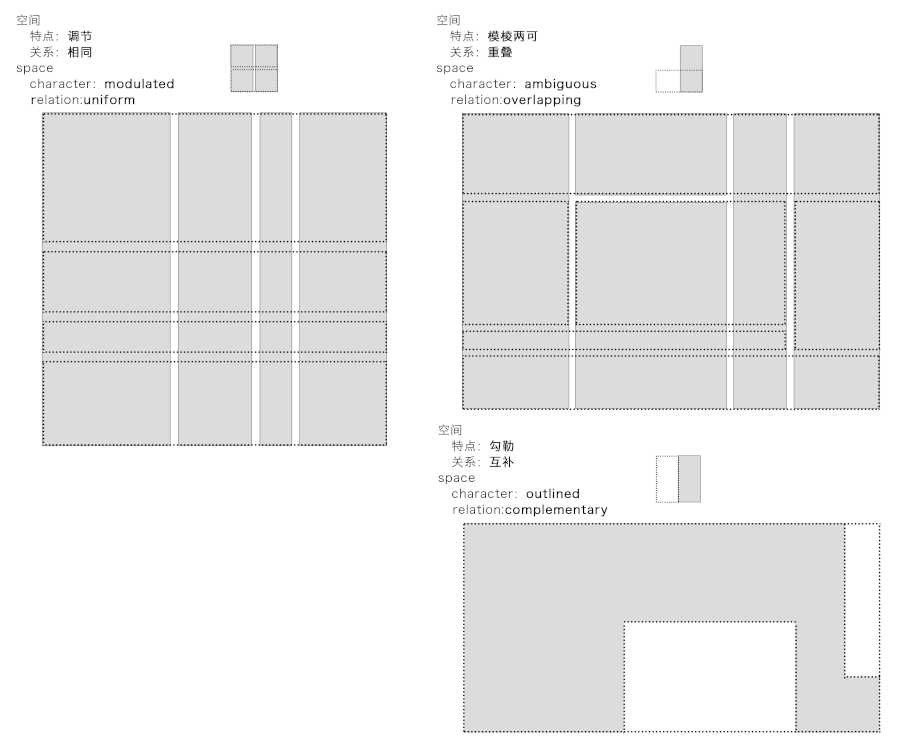
體塊、板片與桿件Volumes, slabs and poles
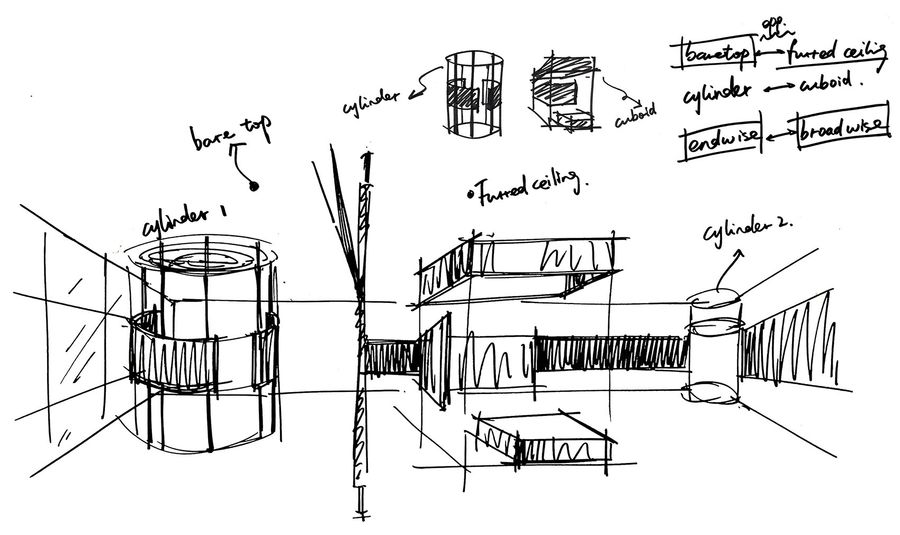
這三種要素所形成的空間具有不同的特點(diǎn),相對(duì)于體塊,實(shí)體與虛空、圖與底處于平衡的關(guān)系,而空間具有明確的邊界。實(shí)體內(nèi)部的空間,以及體塊之間的空間是一種互補(bǔ)的關(guān)系,是“勾勒空間”;相對(duì)于板片,界定出若干相互重疊的空間關(guān)系,空間定位具有“模棱兩可”的特征;相對(duì)于桿件,在空間內(nèi)做疏密或間隔的區(qū)分,具有“調(diào)節(jié)空間”的作用。
▼分析圖,diagram gif ?哇哦設(shè)計(jì)
Different operations on the same material will result in variations of these space types. As the solid,the character of the space is outlined with each space having a clear boundary.The two types of spaces, inside or between the blocks are complementary.The slabs define many spatial zones which overlap,so we call the character of the space ambiguous.Sticks differentiate space from within,so we call the space modulated.We use the terms“outlined space”,“ambiguous space”and“modulated space”for the space types resulting.
▼板片隔斷與體塊坐椅的對(duì)角處理呈現(xiàn)出均衡與穩(wěn)定性the flat partition and the cuboid seat as a diagonal presents to be proportional and stable ?戚朔遷
對(duì)比與統(tǒng)一Contrast & Unity
兩個(gè)空間并未直接用兩種不同材料進(jìn)行區(qū)分,而刻意統(tǒng)一了材質(zhì)。
We used the same material on both spatial dimensions of clothing shop instead of two kinds of material.
▼幾何元素的穿插與交織,geometric elements interweave in the space ?戚朔遷
材料在視覺上令人愉悅的一致性,讓人感受到兩個(gè)空間的協(xié)調(diào)性,同時(shí)又使用了兩個(gè)對(duì)比性形體——圓柱與方體分別作為空間中心,以此強(qiáng)調(diào)人們?cè)诓煌误w關(guān)系中的不同體驗(yàn)感。
In this way, it is not only having a strong visual unify of comfort but also feeling harmony of two spaces,and then includes two forms as the center ——cylinder and cuboid,to emphasize a variety of experience In different physical relations.
▼幾何感的陳列空間, geometrical display space ?戚朔遷
平衡與強(qiáng)調(diào)Balance & Emphasis
面積相似的兩個(gè)區(qū)域用玻璃隔斷分割,對(duì)稱平衡中具有相同的空間特征——周圍用藝術(shù)涂料,中心為穿孔不銹鋼形體,圓柱形體中設(shè)置了6根圓柱,以此強(qiáng)調(diào)其縱向關(guān)系。方形形體中,長(zhǎng)條的隔板與坐椅強(qiáng)調(diào)了其橫向關(guān)系,以此創(chuàng)建興趣中心和視覺焦點(diǎn)。
The partition of toughened glass split in two similar pieces,the well-balanced symmetrical spaces are similar —— We used textural art paint around the spaces and put the boring a hole with stainless steel in central area. Six cylinders are crammed intocylinder in order to emphasize vertical relationship. Linear partition and bench tried to emphasize horizontal relation. It structure the visual focus and interest center in this manner.
▼曲面暗示出不同的功能分區(qū),curve hinted the different functional partition ?戚朔遷
▼無常的曲線賦予空間恣意生長(zhǎng)的可能irregular curve give the possibility of growing-wild space ?戚朔遷
材質(zhì)選擇上,整體以灰色為基調(diào),諸如藝術(shù)涂料、發(fā)泡鋁、不銹鋼等,以凸顯服飾本身的材質(zhì)及色彩,并中和整體空間的冷色基調(diào)。
The choice of material is basic color gray,in order to impress the material quality and the color of clothes,for instance, textural art paint, aluminum foam,stainless steel etc.
▼細(xì)部,details ?戚朔遷
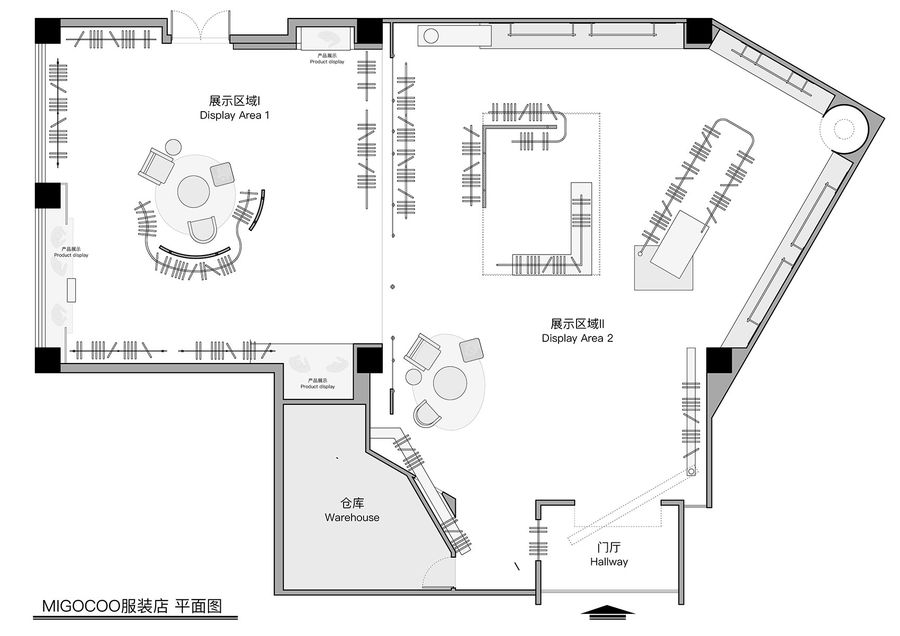
▼平面圖,plan ?哇哦設(shè)計(jì)
項(xiàng)目名稱:MIGOCOO服裝店
項(xiàng)目類型:服裝店鋪
設(shè)計(jì)方:杭州哇哦設(shè)計(jì)有限公司
項(xiàng)目設(shè)計(jì):2022.03
完成年份:2022.07
設(shè)計(jì)團(tuán)隊(duì):張靖琪 蔣冠航 曾亞芳
項(xiàng)目地址:浙江省嘉興市
建筑面積:320㎡
攝影版權(quán):奧觀視覺 戚朔遷
客戶:MIGOCOO材
料:不銹鋼、發(fā)泡鋁、藝術(shù)涂料
更多相關(guān)內(nèi)容推薦























評(píng)論(0)